History of Math-- Discovery of Irrational Numbers

By: Jesse Ding

Math is one of the most well-known subjects in school. Have you ever looked down at your worksheet and wondered how a certain mathematical concept came to be? No? Ok. Trust me, it’s always a fascinating story regarding how certain mathematical concepts came to be. The discovery of irrational numbers is no exception. Have you heard about irrational numbers? These are numbers that cannot be expressed as a ratio between two numbers. One example being π––the ratio between the circumference and diameter of a circle. The discovery of irrational numbers is a discovery that forever shook the world of math and is a discovery who’s inventor suffered from.

Pythagoras. The famous Greek Philosopher and Mathematician. You might know him through his famous Pythagorean Theorem (a^2+b^2=c^2)––which expresses the relation between the three sides of a right triangle––or the cult/belief that he started––Pythagoreanism. In his middle ages, Pythagoras settled in Croton, Southern Italy, where he established his school. Members of the school were taught and pursued studies of Math, Philosophy, Astronomy, and Music. The school’s teachings and knowledge were kept secret from the public: everything was taught verbally and notetaking was not allowed.

Pythagoras and those who followed in his footsteps believed that “All is Number.” and that Math was not something to study on its own, but it is a key to all the secrets of the universe. The Pythagoreans attributed significance to their ability to perceive the presence of rational numbers in everything, whether it was a sunrise, the stars in the sky, human nature, or a musical composition.

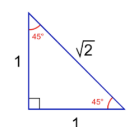
Hippasus, a Pythagorean Mathematician/Philosopher, is credited for the discovery of irrational numbers. Using the Pythagorean Theorem (a^2+b^2=c^2), he assigned the values of a and b to be 1; when substituting these values into the equation, you’ll get 1^2+1^2=c^2, any power 1 is brought up to is still one, 1+1=c^2, adding 1 and 1 together will then result in this equation, 2=c^2, now the important part: since 2 is equal to c squared, taking the square root of both sides will result in c being √2.

Many frantic attempts later, it was declared that no ratio between two numbers could produce √2. This was a true shock to the Pythagorean Mathematicians; imagine proving that 2+2=5 or that 10 was odd, it sounds like something that can’t be done, but that’s how it must have been for many at the time of the discovery: the finding of the impossible. However, was this discovery well received? You’d imagine finding such a discovery would be a prestigious achievement, but that would be wrong. Although the truth is heavily clouded, many speculate that that Pythagoras sentenced Hippasus to death by drowning for such a crime.

The message to take away from this is that you should never be afraid to explore the impossible; the next time when you see something out there in the world, you may discover a hidden chapter of the world’s history. So take out your thinking cap and being curious!

Proof that √2 is Irrational

By: Hippasus

First, let √2 be rational, thus it can be expressed as a ratio between two numbers, let that ratio be p/q

If p/q is the ratio, that means that they cannot share any common factors

With those two rules, we can write the equation, √2=p/q

Next, we can multiply both sides by q, resulting in the equation that √2q=p (2q is not being square rooted, only 2 is)

Squaring both sides of the equation will then results in (√2q)^2=p^2, when simplified, it results in, 2q^2=p^2

Some side knowledge: All even numbers are even when squared and all even numbers are multiples of 2. So looking back at the equation, 2q^2=p^2, we know that both sides of the equation are even, as 2 times any number is even, in this case, 2 times q^2, and that any even number squared is even

Knowing that, we can conclude that p is even

Let p can be expressed as 2a––as any even number can be expressed as 2 times another integer.

Substituting 2c for p in the equation where we left off––2q^2=p^2––we get 2q^2=(2a)^2, which equals 2q^2=4a^2

Dividing both sides by 2, the equation then turns into q^2=2a^2, going back to the rules of even integers, 2 times any number is even, so 2 times a^2 is even, and any even number squared is even

That means that q is even as well

However, since both integers in the ratio p/q are even, that contradicted our fundamental statement that they do not share any common factors: as all even numbers have a common factor of 2

Thus, this means that √2 is irrational.

What Hippasus used here is called a “Proof by Contradiction”.